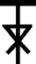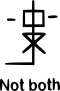In logic, a logical connective (also called a logical operator, sentential connective, or sentential operator) is a logical constant used to connect two or more formulas. For instance in the syntax of propositional logic, the binary connective {\displaystyle \lor }\lor can be used to join the two atomic formulas {\displaystyle P} P and {\displaystyle Q} Q, rendering the complex formula {\displaystyle P\lor Q}P\lor Q.
Common connectives include negation, disjunction, conjunction, and implication. In standard systems of classical logic, these connectives are interpreted as truth functions, though they receive a variety of alternative interpretations in nonclassical logics. Their classical interpretations are similar to the meanings of natural language expressions such as English not, or, and, and if, but not identical. Discrepancies between natural language connectives and those of classical logic have motivated nonclassical approaches to natural language meaning as well as approaches which pair a classical compositional semantics with a robust pragmatics.
| English word | mantrakshar | Connective | Venn Diagram | Symbol | Logical gate |
| not | 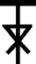 | Negation | | ¬ | NOT |
| and |  | Conjunction |  | ∧ | AND |
| not both | 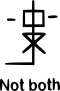 | Alternative denial |  | ↑ | NAND |
| or |  | Disjunction |  | ∨ | OR |
| neither…nor |  | Joint denial | 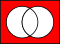 | ↓ | NOR |
| if…then |  | Material implication |  | → | IMPLY |
| one or the other but not both | | Exclusive or |  | | XOR |
| if and only if |  | Biconditional |  | ↔ | XNOR |
| …if |  | Converse implication |  | ← | |
| but not |  | material nonimplication | | ↛ | NIMPLY |
| | | | | | |
| | | | | | |
| | | | | | |
| left is less than right |  | left < right |
| left is more than right | 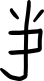 | left > right |
| right is less than left |  | right < left |
| right is more than left |  | right > left |
| | | EXAMPLE IDEOGRAM | |
| truth / tautology | | box | |
| falsify / contradiction | | not box | |
| proposition P | | left | |
| Negation | | not left | |
| Proposition P and Q | | | |
| proposition P true | | left is true | |
| proposition Q True | | right is true | |
| propositon p and q | Conjunction | left and right is true , only if left is true and right is true , otherwise it is false | AND |
| | Alternative denial | not left and not right is the correct output , if either left or right are not correct | NAND (not and ) |
| | | left or right is correct output , if left is correct input or right is correct input | |
| | | | |
| | | | |